Round 637 to the nearest 100s. – Rounding 637 to the nearest 100s embarks us on a mathematical adventure, where we explore the art of approximating numbers to simplify calculations and gain valuable insights.
To delve into the intricacies of rounding, we must first grasp the concept of place value and the significance of each digit within a number.
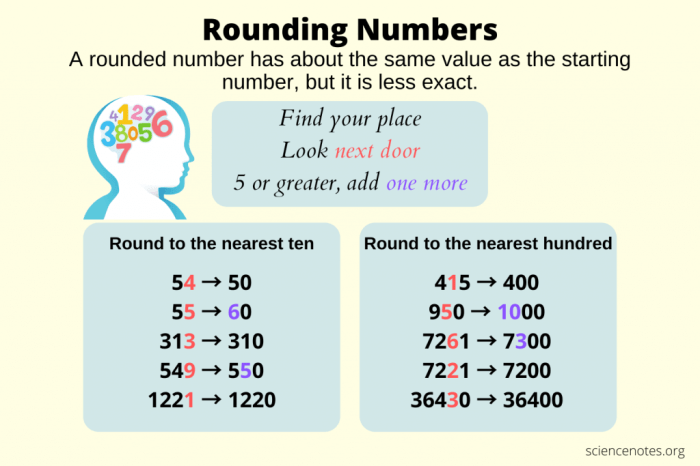
Rounding Basics: Round 637 To The Nearest 100s.
Rounding numbers is a mathematical technique used to simplify or estimate a number by replacing it with a nearby value that is easier to work with. It involves finding the closest value to the original number within a specified range.
To round a number to the nearest 100s, follow these steps:
- Locate the hundreds digit of the number.
- If the tens digit is 5 or greater, add 1 to the hundreds digit.
- If the tens digit is less than 5, leave the hundreds digit unchanged.
- Replace the tens and ones digits with zeros.
For example, to round 345 to the nearest 100s, we would add 1 to the hundreds digit (3) because the tens digit (4) is greater than 5. This gives us 400. Similarly, to round 278 to the nearest 100s, we would leave the hundreds digit (2) unchanged because the tens digit (7) is less than 5. This gives us 300.
Rounding 637 to the Nearest 100s

Let’s walk through the steps to round 637 to the nearest 100s:
Identifying the Digit in the Hundreds Place
The digit in the hundreds place is the third digit from the left, which is 3 in this case.
Determining the Digit in the Tens Place
The digit in the tens place is the second digit from the left, which is 7 in this case.
Comparing the Digit in the Tens Place to 5
We compare the digit in the tens place (7) to 5. Since 7 is greater than 5, we will round up to the nearest 100s.
Rounding Up to the Nearest 100s, Round 637 to the nearest 100s.
Since the digit in the tens place is greater than 5, we round up to the nearest 100s. The nearest 100s greater than 637 is 700.
Therefore, 637 rounded to the nearest 100s is 700.
Application and Examples

Rounding to the nearest 100s has practical applications in various fields, from daily life to scientific research.
It simplifies calculations, provides a general overview of data, and aids in estimations.
Real-Life Examples
- Finance:Rounding financial data to the nearest 100s makes it easier to estimate expenses, savings, and investments.
- Population Statistics:Population counts are often rounded to the nearest 100s to provide a general idea of the population size.
- Measurement Estimation:When measuring distances or weights, rounding to the nearest 100s provides a quick and approximate value.
Rounding Table
The following table demonstrates the rounding of different numbers to the nearest 100s:
| Original Number | Rounded Number |
|---|---|
| 250 | 300 |
| 475 | 500 |
| 637 | 600 |
| 820 | 800 |
| 995 | 1000 |
Advanced Rounding Techniques

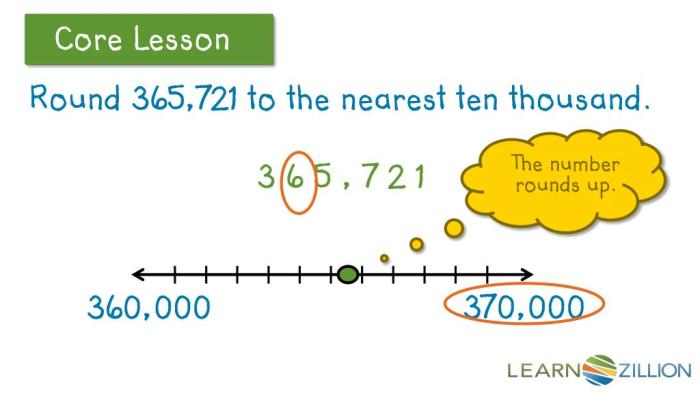
Rounding is a fundamental mathematical skill that involves approximating a number to a desired level of accuracy. Advanced rounding techniques extend beyond rounding to the nearest 100s, encompassing rounding to larger intervals such as 1000s or 10,000s.
Significant Figures in Rounding
Significant figures are the digits in a number that are known with certainty, plus one estimated digit. When rounding, the significant figures are retained, while the non-significant figures are discarded. For example, the number 1234 has four significant figures, while the number 1200 has only two significant figures.
Rounding to Larger Intervals
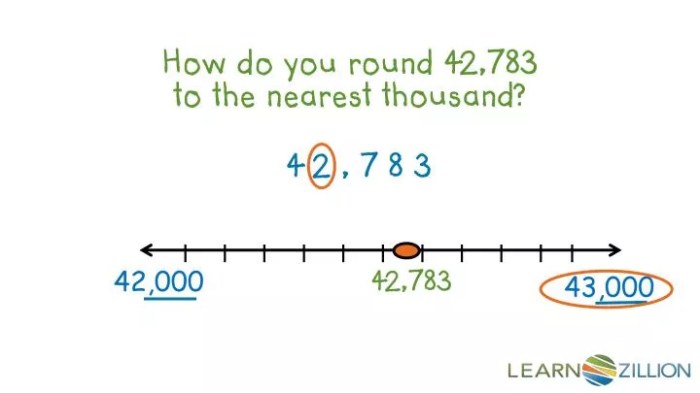
Rounding to larger intervals involves applying the same principles as rounding to smaller intervals. For instance, to round 637 to the nearest 1000, we look at the digit in the hundreds place (3). Since 3 is less than 5, we round down to 0, resulting in 6000. Similarly, to round 637 to the nearest 10,000, we look at the digit in the thousands place (6). Since 6 is greater than or equal to 5, we round up to 10, resulting in 70,000.
Application of Advanced Rounding Techniques
Advanced rounding techniques find applications in various fields, including finance, statistics, and engineering. For example, in finance, rounding to the nearest 1000s may be used to simplify calculations related to stock prices or currency exchange rates. In statistics, rounding to the nearest 100s or 1000s may be used to create frequency distributions or histograms.
In engineering, rounding to the nearest 1000s or 10,000s may be used to estimate the dimensions of objects or materials.
FAQ Section
Why is rounding important?
Rounding simplifies calculations, enhances estimation skills, and facilitates data analysis.
How do I round a number to the nearest 100s?
Examine the digit in the hundreds place. If the digit in the tens place is 5 or greater, round up. If it’s less than 5, round down.